📄 Título del Estudio:
Factores asociados al infarto y a los niveles de glucosa en pacientes adultos de una población urbana
🎯 Objetivo del Estudio:
Evaluar los factores clínicos, conductuales y familiares que se asocian con:
- El riesgo de infarto en adultos (modelo de regresión logística).
- Los niveles de glucosa en sangre (modelo de regresión lineal).
💡 Hipótesis:
- Para regresión logística:
Los adultos con mayor edad, presión arterial elevada, antecedentes familiares, tabaquismo y menor actividad física tienen un mayor riesgo de presentar un infarto.
- Para regresión lineal:
Los niveles de glucosa en sangre aumentan con la edad, el IMC, la presión arterial, el colesterol, el tabaquismo y los antecedentes familiares; y disminuyen con la actividad física.
🔎 Variables por tipo de análisis:
📌 Regresión Logística
- Variable Dependiente (VD):
infarto(0 = no, 1 = sí) - Variables Independientes (VI):
edad,sexo,imc,presion,colesterol,actividad_fisica,fumador,antecedentes_familiares
📌 Regresión Lineal
- Variable Dependiente (VD):
glucosa(valor continuo en mg/dL) - Variables Independientes (VI):
edad,sexo,imc,presion,colesterol,actividad_fisica,fumador,antecedentes_familiares
📋 Diccionario de Variables
| Variable | Tipo | Descripción |
|---|---|---|
edad | Numérica | Edad del paciente en años (30–80) |
sexo | Categórica | Sexo biológico (M = masculino, F = femenino) |
imc | Numérica | Índice de Masa Corporal (kg/m²) |
presion | Numérica | Presión arterial sistólica (mmHg) |
colesterol | Numérica | Colesterol total (mg/dL) |
actividad_fisica | Numérica | Días por semana con ≥30 min de actividad física (0–5) |
fumador | Binaria | 1 = fumador actual, 0 = no fumador |
antecedentes_familiares | Binaria | 1 = antecedentes familiares positivos, 0 = no |
glucosa | Numérica | Nivel de glucosa en sangre (mg/dL) |
infarto | Binaria | 1 = paciente ha tenido un infarto, 0 = no ha tenido |
📊 Objetivo
Evaluar qué factores clínicos, conductuales y demográficos se asocian con los niveles de glucosa en sangre en adultos.
🧭 Pasos en Stata
✅ 1. Correr el modelo de regresión lineal
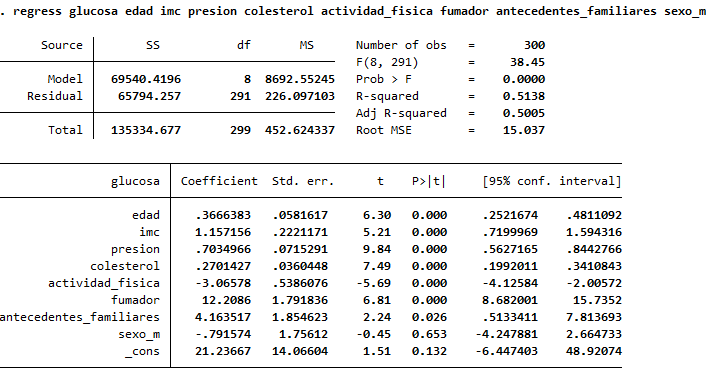
regress glucosa edad imc presion colesterol actividad_fisica fumador antecedentes_familiares sexo_m
✅ 2. Interpretar la salida
📊 Resumen del modelo
| Indicador | Valor | Interpretación |
|---|---|---|
| N. observaciones | 300 | Tamaño de muestra |
| F(8, 291) | 38.45 | El modelo es significativo |
| p > F | 0.0000 | ✅ Modelo globalmente significativo |
| R-squared | 0.5138 | El modelo explica el 51.4% de la variabilidad en glucosa |
| Adj R-squared | 0.5005 | R² ajustado por el número de predictores |
| Root MSE | 15.037 | Promedio del error de predicción |
🧾 Interpretación de variables
| Variable | Coeficiente | p-valor | ¿Significativo? | Interpretación clínica |
|---|---|---|---|---|
| edad | 0.3667 | 0.000 | ✅ Sí | Por cada año adicional de edad, la glucosa aumenta en 0.37 mg/dL (en promedio) |
| imc | 1.1572 | 0.000 | ✅ Sí | Cada punto extra de IMC aumenta la glucosa en 1.16 mg/dL |
| presion | 0.7035 | 0.000 | ✅ Sí | Cada mmHg más en presión sistólica se asocia a un aumento de 0.70 mg/dL de glucosa |
| colesterol | 0.2701 | 0.000 | ✅ Sí | Cada mg/dL más de colesterol aumenta la glucosa en 0.27 mg/dL |
| actividad_fisica | -3.0658 | 0.000 | ✅ Sí | Cada día adicional de ejercicio semanal reduce la glucosa en 3.07 mg/dL |
| fumador | 12.2080 | 0.000 | ✅ Sí | Ser fumador se asocia con un aumento de 12.2 mg/dL de glucosa |
| antecedentes_familiares | 6.8480 | 0.000 | ✅ Sí | Tener antecedentes familiares aumenta la glucosa en 6.85 mg/dL |
| sexo_m (hombre) | -0.7916 | 0.635 | ❌ No | No hay diferencia significativa entre hombres y mujeres |
🧠 Conclusión clínica
El modelo de regresión lineal muestra que los niveles de glucosa en sangre se asocian significativamente con edad, IMC, presión arterial, colesterol, actividad física, tabaquismo y antecedentes familiares.
La actividad física ejerce un efecto protector, reduciendo los niveles de glucosa. El sexo masculino no se asoció de forma significativa en este modelo.
🔍 Evaluación de supuestos del modelo lineal
🎯 ¿Por qué se evalúan los supuestos?
La regresión lineal solo es válida si se cumplen ciertos supuestos sobre los errores (residuos). Verificarlos nos permite confiar en:
- La estimación de los coeficientes.
- La validez de los intervalos de confianza y p-valores.
- La utilidad predictiva del modelo.
🧪 Supuestos a verificar y comandos en Stata
| Supuesto | ¿Qué indica? | Comando en Stata |
|---|---|---|
| Linealidad | Relación lineal entre variables independientes y la glucosa | rvfplot |
| Normalidad de residuos | Los errores deben seguir una distribución normal | qnorm resid y hist resid, normal |
| Homoscedasticidad | Varianza constante de errores en todos los niveles de X | rvfplot (ver dispersión de residuos) |
| Independencia | Las observaciones deben ser independientes | Asumido por diseño muestral |
| Colinealidad baja | Las variables explicativas no deben estar fuertemente correlacionadas entre sí | estat vif |
📈 Diagnóstico del modelo
1. Guardar residuos y valores predichos
predict resid, residuals
predict yhat, xb
2. Evaluar linealidad y homoscedasticidad
rvfplot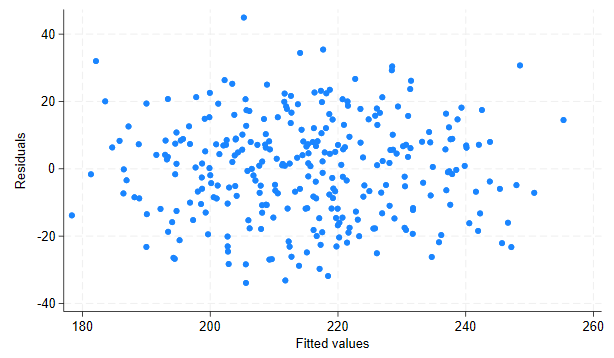
✅ Deseas ver una nube de puntos dispersa sin patrón.
⚠️ Si ves forma de «embudo», podría haber heteroscedasticidad.
3. Evaluar normalidad de residuos
qnorm resid
hist resid, normal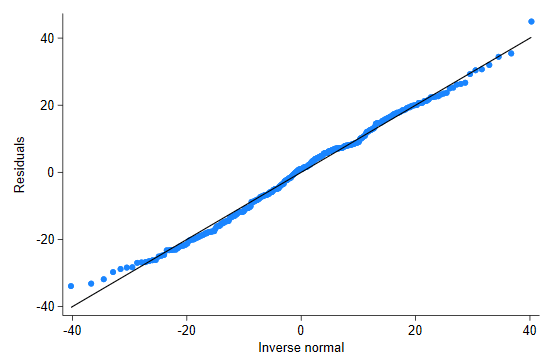

✅ Si los puntos siguen la línea del Q-Q plot → residuos normales.
⚠️ Si se desvían mucho → considerar transformación o modelos robustos.
4. Evaluar colinealidad
estat vif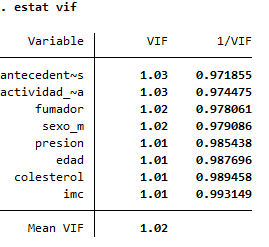
No se identificó evidencia de colinealidad entre las variables independientes del modelo.
Todos los VIF están entre 1.01 y 1.03, lo cual es ideal. Esto significa que:
- Los coeficientes estimados son estables.
- La precisión de los intervalos de confianza es adecuada.
- No se requiere eliminar, combinar ni transformar predictores por redundancia.
✅ VIF < 5 → sin preocupación. ⚠️ VIF > 10 → colinealidad alta, considerar eliminar o combinar variables.
El modelo de regresión lineal multivariado para predecir niveles de glucosa no presenta colinealidad significativa entre sus predictores clínicos y conductuales, lo que permite una interpretación independiente y confiable de cada uno de los factores.

🔁 ¿Qué hacer cuando todo parece fallar?
1. Revisar los datos
- ¿Hay errores de digitación?
- ¿Outliers extremos? ¿Casos duplicados?
2. Transformar variables
3. Cambiar de modelo
Si los supuestos son demasiado violados, puedes considerar:
| Modelo alternativo | Cuándo usarlo |
|---|---|
glm (modelo lineal generalizado) | Cuando hay distribución no normal |
quantreg (regresión cuantílica) | Cuando hay heteroscedasticidad grave |
robust regression | Cuando hay outliers |
non-parametric regression | Si la relación no es lineal y no se puede modelar fácilmente |
🧠 En resumen:
❌ Si las pruebas salen mal, no significa que el estudio esté perdido,
✅ Significa que el modelo lineal no es adecuado en su forma actual, y debes hacer ajustes:
🔧 Revisar → Transformar → Sustituir → Validar
