3.1. Desenlaces primarios y secundarios
3.2. Medidas de efecto: RR, OR, HR, NNT, NNH
3.3. Intervalos de confianza y p-valores
3.4. Subgrupos y análisis por intención de tratar (ITT) vs. por protocolo
3.5. Gráficos de supervivencia y curvas de Kaplan–Meier

3.1. DESENLACES PRIMARIOS Y SECUNDARIOS

Introducción

Los desenlaces (outcomes) son la esencia de un ensayo clínico. Representan las variables de interés que se miden para determinar si una intervención tiene impacto sobre la salud.

El desenlace primario es el centro del estudio, la variable que justifica el diseño, el tamaño muestral y la hipótesis principal.
Los desenlaces secundarios ofrecen información adicional, exploratoria o complementaria, que permite entender mejor los efectos de la intervención.

👉 En medicina basada en evidencia, comprender cómo se definen, clasifican e interpretan los desenlaces es tan importante como el resultado mismo, porque un ensayo puede estar bien diseñado, pero perder relevancia si mide lo que no importa para el paciente.

Breve historia del concepto

Ensayos tempranos (siglo XVIII–XIX): desenlaces eran observaciones clínicas subjetivas (ej. mejora de síntomas en escorbuto con cítricos).
Primeros ensayos controlados (1940s): MRC trial sobre estreptomicina en tuberculosis → usaron mortalidad y mejoría radiográfica como desenlaces.
Década de 1980–90: auge de desenlaces sustitutos (ej. presión arterial, colesterol, HbA1c). Algunos resultaron válidos, otros llevaron a errores clínicos (ej. CAST trial: supresión de arritmias aumentó mortalidad).
Actualidad: CONSORT y ClinicalTrials.gov exigen registrar los desenlaces primarios y secundarios antes de iniciar el ensayo, para evitar manipulación de resultados (outcome switching).

Desenlace primario

Definición

Es la variable principal que un ensayo pretende evaluar. Todo el diseño del estudio (cálculo muestral, hipótesis estadística, análisis principal) gira en torno a este desenlace.

Características ideales

Clínicamente relevante: debe reflejar beneficios reales para el paciente (ej. mortalidad, hospitalización, calidad de vida).
Objetivo y medible: minimizar subjetividad.
Definido con claridad: evitar interpretaciones ambiguas.
Preespecificado: registrado antes del inicio del ensayo.
Único o compuesto: puede ser un solo evento (ej. mortalidad total) o la combinación de varios (ej. MACE en cardiología: IAM, ACV, muerte CV).

Ejemplos

DAPA-HF (2019): desenlace primario = compuesto de empeoramiento de IC o muerte CV.
HOPE (2000): muerte CV, IAM no fatal, ACV.
UKPDS (1998): HbA1c (sustituto) y complicaciones microvasculares.

Desenlaces secundarios

Definición

Son variables adicionales que complementan al primario:

Exploran otros posibles beneficios.
Evalúan seguridad y tolerancia.
Generan hipótesis para estudios futuros.

Ejemplos

En EMPA-REG OUTCOME (2015): el primario fue un compuesto CV, y los secundarios incluyeron hospitalización por IC → hallazgo que luego dio origen a estudios específicos en IC.
En DAPA-HF: además del desenlace primario, se midió mortalidad total, hospitalizaciones repetidas y calidad de vida (KCCQ).

Limitaciones

Multiplicidad de comparaciones aumenta riesgo de error tipo I (falsos positivos).
Si el desenlace primario es negativo, los secundarios deben interpretarse con mucha cautela.

Tipos de desenlaces

1. Desenlaces clínicos “duros” (hard outcomes)

Eventos mayores e inequívocos: mortalidad, IAM, ACV, hospitalización.
Alta relevancia clínica.
Ejemplo: mortalidad total en SOLVD trial (enalapril en IC).

2. Desenlaces compuestos

Combinan varios eventos en uno solo.
Ventajas: aumentan poder estadístico, reducen tamaño muestral.
Riesgos: componentes de diferente importancia pueden distorsionar la interpretación.
Ejemplo: en cardiología, MACE (major adverse cardiovascular events).

3. Desenlaces sustitutos (surrogate endpoints)

Variables intermedias que predicen un evento clínico.
Ejemplos: LDL en dislipidemia, HbA1c en diabetes, presión arterial en HTA.
Riesgo: no siempre se correlacionan con beneficio real.
- Ejemplo negativo: rosiglitazona reducía HbA1c, pero aumentaba riesgo CV.
- Ejemplo positivo: reducción de LDL con estatinas sí se correlaciona con menos IAM y muerte CV.

4. Desenlaces de calidad de vida y funcionalidad

Usan escalas validadas: EQ-5D, KCCQ, SF-36.
Importancia creciente en medicina centrada en el paciente.
Ejemplo: ensayos de IC que incluyen mejoría en la clase funcional NYHA y calidad de vida.

Problemas frecuentes

Cambio de desenlace primario (outcome switching):
- Se selecciona como “primario” aquel que salió significativo.
- Riesgo de sesgo de reporte.
- Ejemplo: ensayos que publican resultados favorables en desenlaces secundarios aunque el primario haya sido negativo.
Uso excesivo de desenlaces sustitutos:
- Lleva a decisiones clínicas basadas en parámetros intermedios que no siempre traducen beneficios reales.
Eventos dispares en desenlaces compuestos:
- Si uno domina (ej. hospitalización leve frente a muerte), se distorsiona el efecto.
Subreportar secundarios negativos:
- Ejemplo: reportar solo beneficios secundarios y ocultar desenlaces de seguridad.

Evaluación crítica

Preguntas clave:

¿El desenlace primario es clínicamente relevante?
- ¿Impacta en mortalidad, morbilidad o calidad de vida?
¿Está claramente definido y registrado?
- ¿Se registró en ClinicalTrials.gov antes del inicio?
¿Se usaron sustitutos?
- ¿Existe correlación validada con eventos duros?
¿El desenlace compuesto está bien balanceado?
- ¿Cada componente es relevante y ocurre con frecuencia comparable?
¿Qué papel juegan los secundarios?
- ¿Confirmaron hallazgos o solo generaron hipótesis?

Ejemplos emblemáticos

HOPE (2000): desenlace primario sólido (IAM, ACV, muerte CV). Cambió práctica clínica.
CAST (1989): desenlace sustituto (supresión de arritmias ventriculares). Resultado: más mortalidad → ejemplo de sustituto engañoso.
RECOVERY (2020): primario = mortalidad a 28 días en COVID-19 hospitalizados. Resultado: dexametasona redujo mortalidad. Ejemplo de desenlace claro, simple y clínicamente importante.
EMPA-REG (2015): el hallazgo secundario de hospitalización por IC abrió un nuevo campo de investigación para los iSGLT2.

Tabla comparativa

Tipo de desenlace	Definición	Ventaja	Limitación	Ejemplo
Primario	Variable principal del estudio	Potencia estadística, relevancia	Si es irrelevante, invalida ensayo	HOPE: IAM, ACV, muerte CV
Secundario	Variables adicionales	Complementan eficacia y seguridad	Riesgo de falsos positivos	EMPA-REG: hospitalización IC
Compuesto	Combina eventos	Reduce tamaño muestral	Componentes desiguales distorsionan	MACE en cardiología
Sustituto	Biomarcador intermedio	Fácil, rápido	No siempre refleja beneficio real	HbA1c en DM2, LDL en dislipidemia
Calidad de vida	Escalas validadas	Enfoque centrado en el paciente	Subjetividad, logística	KCCQ en IC

3.2. MEDIDAS DE EFECTO: RR, OR, HR, NNT, NNH

Introducción

Las medidas de efecto son los indicadores que convierten los resultados de un ensayo clínico en información cuantitativa y clínicamente interpretable. No basta con decir que un tratamiento “funciona” o que la diferencia es “estadísticamente significativa”: lo que importa es cuánto mejora el pronóstico del paciente y a qué costo en seguridad.

Estas medidas permiten:

Traducir resultados a probabilidades concretas.
Comparar magnitudes entre diferentes intervenciones.
Facilitar la comunicación con pacientes y colegas en términos claros.

👉 En síntesis: son el lenguaje numérico de la medicina basada en evidencia (MBE).

Bases conceptuales y matemáticas

Todo cálculo parte de una tabla 2×2 (para desenlaces binarios: evento sí/no).

	Evento (+)	Evento (–)	Total
Intervención	a	b	a+b
Control	c	d	c+d

Riesgo en intervención = a / (a+b)
Riesgo en control = c / (c+d)

A partir de estas proporciones se derivan:

Riesgo Relativo (RR)
Reducción Absoluta del Riesgo (RAR)
Número Necesario a Tratar (NNT)
Odds Ratio (OR)
Y en análisis de tiempo → Hazard Ratio (HR)

1. Riesgo Relativo (RR)

Definición

El RR compara la probabilidad de un evento entre el grupo intervención y el grupo control:

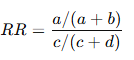
Interpretación

RR = 1: no hay diferencia.
RR < 1: el tratamiento reduce el riesgo.
RR > 1: el tratamiento aumenta el riesgo.

Ejemplo clínico

En un ensayo de prevención cardiovascular:

Mortalidad con placebo = 10%
Mortalidad con fármaco = 7%

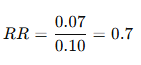
→ La intervención redujo la mortalidad en un 30% relativo.

👉 Ventaja: intuitivo, útil para comunicar en consulta.

2. Odds Ratio (OR)

Definición

El OR compara la probabilidad de evento frente a no evento en ambos grupos.

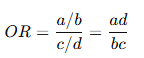
Interpretación

OR = 1: no hay diferencia.
OR < 1: la intervención reduce odds de evento.
OR > 1: la intervención aumenta odds de evento.

Ejemplo clínico

Intervención: 40% éxito; Control: 20% éxito.

Odds intervención = 0.4/0.6 = 0.67
Odds control = 0.2/0.8 = 0.25

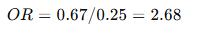
→ El tratamiento multiplica por 2.7 la probabilidad de éxito.

👉 Importante: cuando los eventos son comunes (>10%), el OR tiende a sobreestimar el efecto respecto al RR.

3. Hazard Ratio (HR)

Definición

El HR es una medida dinámica: compara las tasas de ocurrencia de eventos en el tiempo entre dos grupos, usando análisis de supervivencia (modelo de Cox).

Interpretación

HR = 1: no hay diferencia en riesgo a lo largo del tiempo.
HR < 1: menor tasa de eventos con la intervención.
HR > 1: mayor tasa de eventos con la intervención.

Ejemplo clínico

En DAPA-HF (2019):

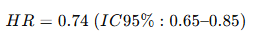
→ Dapagliflozina redujo en un 26% el riesgo relativo de empeoramiento de IC o muerte CV durante 18 meses.

👉 Ventaja: incorpora el tiempo hasta el evento, no solo si ocurrió o no.

4. Número Necesario a Tratar (NNT)

Definición

El NNT indica cuántos pacientes deben recibir el tratamiento para prevenir un evento adicional en comparación con el control.

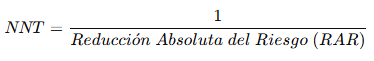
Ejemplo clínico

Con placebo: mortalidad 10%.
Con tratamiento: mortalidad 7%.

RAR = 0.10 – 0.07 = 0.03 (3%).
NNT = 1 / 0.03 = 33.

→ Se deben tratar 33 pacientes durante 2 años para salvar 1 vida.

👉 Es una medida clínicamente tangible para guiar decisiones.

5. Número Necesario para Dañar (NNH)

Definición

Es el número de pacientes que deben recibir la intervención para que ocurra un evento adverso adicional respecto al control.

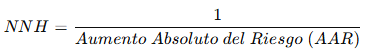
Ejemplo clínico

EA en control = 5%.
EA en intervención = 9%.
AAR = 0.09 – 0.05 = 0.04 (4%).
NNH = 1 / 0.04 = 25.

→ Por cada 25 pacientes tratados, 1 sufrirá un efecto adverso atribuible al fármaco.

Relación NNT vs. NNH

El valor real de una intervención emerge al comparar beneficio y riesgo.

Ejemplo:

NNT = 33 para prevenir una muerte.
NNH = 200 para causar un sangrado mayor.
👉 El balance beneficio-riesgo favorece el uso de la terapia.

En cambio, si NNT ≈ NNH, la decisión clínica debe individualizarse según valores y preferencias del paciente.

Críticas y limitaciones

RR y OR: no expresan riesgo absoluto → riesgo de “exagerar” beneficios.
OR: malinterpretado como RR en eventos frecuentes.
HR: asume proporcionalidad de riesgos, lo cual no siempre se cumple si las curvas se cruzan.
NNT y NNH: dependen del horizonte temporal y del riesgo basal → varían según población.
Interpretación aislada: ningún indicador debe leerse sin contexto clínico ni sin intervalos de confianza.

Ejemplos emblemáticos

HOPE trial (2000):
- Ramipril redujo eventos CV:
- RR 0.78; RAR 1.8% anual; NNT = 56 en 5 años.
RECOVERY (COVID-19, 2020):
- Dexametasona redujo mortalidad en ventilados:
- RR 0.65; NNT = 8 a 28 días.
CAST trial (1989):
- Antiarrítmicos reducían arritmias (sustituto), pero aumentaban mortalidad (NNH bajo) → ejemplo clásico de que el beneficio aparente puede revertirse al evaluar desenlaces clínicos.

Tabla comparativa

Medida	Definición	Ventaja	Limitación	Ejemplo
RR	Riesgo en intervención vs. control	Intuitivo, clínico	No expresa magnitud absoluta	HOPE: RR 0.78
OR	Odds de evento entre grupos	Útil en casos-control	Sobreestima con eventos comunes	Ensayos pequeños
HR	Tasa de eventos en el tiempo	Incorpora tiempo hasta evento	Supone proporcionalidad	DAPA-HF: HR 0.74
NNT	Pacientes necesarios para beneficiar a 1	Fácil de aplicar	Depende de riesgo basal y tiempo	RECOVERY: NNT=8
NNH	Pacientes necesarios para dañar a 1	Evalúa seguridad	Varía entre poblaciones	CAST: NNH bajo

3.3. INTERVALOS DE CONFIANZA Y P-VALORES

Introducción

En los ensayos clínicos, los resultados estadísticos se suelen reportar mediante p-valores y intervalos de confianza (IC). Ambos conceptos están íntimamente relacionados, pero ofrecen perspectivas distintas:

El p-valor responde a la pregunta: ¿es probable que este resultado se deba al azar si la hipótesis nula es cierta?
El intervalo de confianza responde: ¿en qué rango de valores podría estar el verdadero efecto del tratamiento, con un nivel de certeza dado?

👉 Una lectura crítica requiere ir más allá del p<0.05 y analizar si el IC muestra un efecto preciso, consistente y clínicamente relevante.

Breve historia del p-valor y los IC

1925: Ronald A. Fisher introduce el concepto de nivel de significancia (p<0.05 como criterio arbitrario de evidencia).
1930s: Jerzy Neyman y Egon Pearson desarrollan la teoría de hipótesis nula, errores tipo I y II, y proponen intervalos de confianza como complemento.
Décadas posteriores: el uso exclusivo de p-valores se convierte en estándar, pero surge crítica por su malinterpretación.
Hoy: CONSORT y guías de revistas médicas recomiendan reportar siempre medidas de efecto con IC al 95%, más allá del p-valor.

1. P-VALORES

Definición

El p-valor es la probabilidad de obtener un resultado igual o más extremo que el observado, asumiendo que la hipótesis nula es cierta.

Interpretación práctica

p < 0.05: evidencia estadísticamente significativa → se rechaza la hipótesis nula.
p ≥ 0.05: no hay evidencia suficiente para rechazar la hipótesis nula.

Limitaciones

No mide magnitud del efecto: un resultado trivial puede ser “significativo”.
No mide relevancia clínica: un fármaco puede bajar la presión 1 mmHg con p<0.001, lo cual carece de importancia práctica.
No mide probabilidad de hipótesis: un p=0.04 no significa que haya 96% de probabilidad de que la intervención funcione.
Dependencia del tamaño muestral:
- Ensayo gigante → diferencias pequeñas serán significativas.
- Ensayo pequeño → diferencias grandes pueden no alcanzar significancia.

👉 Por sí solo, el p-valor es insuficiente para la toma de decisiones clínicas.

2. INTERVALOS DE CONFIANZA (IC)

Definición

El IC95% es el rango de valores dentro del cual se espera que se encuentre el verdadero efecto de la intervención en el 95% de los estudios repetidos en condiciones similares.

Interpretación

IC que no cruza el valor nulo (1 para RR/OR/HR o 0 para diferencias de medias): resultado significativo.
IC estrecho: alta precisión.
IC amplio: incertidumbre; muestra pequeña o pocos eventos.

Ventajas sobre el p-valor

Indican magnitud del efecto (no solo existencia de diferencia).
Reflejan precisión estadística.
Facilitan evaluar relevancia clínica: no es lo mismo un HR 0.80 con IC 0.79–0.81 (preciso, confiable) que un HR 0.80 con IC 0.50–1.20 (incierto).

3. RELACIÓN ENTRE P-VALOR E IC

Ambos derivan de la misma estadística inferencial:

Si el IC95% excluye el valor nulo, el p < 0.05.
Si el IC95% incluye el valor nulo, el p ≥ 0.05.

👉 La diferencia es que el IC muestra cuánto y con qué grado de certeza, mientras que el p-valor solo dice si hay diferencia o no.

4. Ejemplos clínicos

Ejemplo 1 – Ensayo positivo y preciso

HR = 0.80 (IC95% 0.70–0.92), p=0.003
→ Reducción del 20% en riesgo relativo, consistente y clínicamente relevante.

Ejemplo 2 – Ensayo no concluyente

HR = 0.80 (IC95% 0.55–1.10), p=0.15
→ Puede haber beneficio del 45% o ningún efecto. Muestra imprecisión y falta de poder estadístico.

Ejemplo 3 – Resultado significativo pero irrelevante

Diferencia en PA: –1 mmHg (IC95% –0.8 a –1.2), p<0.001
→ Estadísticamente “significativo”, pero clínicamente irrelevante.

5. Trampas comunes

Dicotomía artificial (p<0.05 vs. p≥0.05): la realidad es un gradiente de evidencia.
P-hacking: manipular análisis hasta lograr p<0.05.
Cambio de desenlaces: reportar secundarios significativos cuando el primario fue negativo.
Confusión entre significancia y relevancia: considerar positivo un hallazgo irrelevante para el paciente.
IC amplios: aunque p<0.05, un IC que abarca desde gran beneficio hasta daño potencial sugiere cautela.

6. Ejemplos emblemáticos

HOPE (2000): ramipril redujo eventos CV → RR 0.78 (IC95% 0.70–0.86), p<0.001. Resultado sólido y clínicamente importante.
CAST (1989): supresión de arritmias con antiarrítmicos → IC estrecho, p<0.01, pero mostró aumento de mortalidad. Ejemplo de que un hallazgo estadístico debe analizarse en su contexto clínico.
RECOVERY (2020): dexametasona redujo mortalidad en pacientes ventilados → RR 0.65 (IC95% 0.51–0.82). Preciso, robusto, y cambió práctica clínica en todo el mundo.

Tabla comparativa

Característica	P-valor	Intervalo de confianza
Qué mide	Probabilidad de resultado bajo H₀	Rango plausible del efecto verdadero
Valor nulo	Implícito (p<0.05)	Explícito (ej. RR=1)
Magnitud	No informa	Sí informa
Precisión	No informa	Sí informa (ancho del IC)
Sensibilidad	Muy dependiente del tamaño muestral	Depende de tamaño y variabilidad
Relevancia clínica	Limitada	Alta
Recomendación actual	No usarlo solo	Reportar siempre junto al efecto

3.4. SUBGRUPOS Y ANÁLISIS POR INTENCIÓN DE TRATAR (ITT) VS. POR PROTOCOLO

Introducción

El análisis de un ensayo clínico no se limita a la comparación global entre dos grupos. La validez y aplicabilidad de sus conclusiones dependen de cómo se analizan los datos (ITT vs. PP) y de si se explora la posible variabilidad del efecto en distintos subgrupos de pacientes.

Estos aspectos, aunque técnicos, tienen un impacto clínico enorme:

Un ensayo puede ser válido internamente pero poco aplicable si los resultados solo benefician a un subgrupo específico.
El modo en que se incluyan o excluyan pacientes en el análisis puede cambiar la interpretación de eficacia o seguridad de la intervención.

👉 Son temas que diferencian la lectura crítica de un ensayo clínico de la simple lectura de su resumen.

1. Análisis por subgrupos

Definición

Consiste en evaluar si la magnitud del efecto de una intervención difiere entre categorías de pacientes.

Ejemplos de subgrupos:

Edad (<65 vs. ≥65 años).
Sexo.
Severidad de enfermedad (NYHA II vs. NYHA IV en insuficiencia cardíaca).
Región geográfica (Europa vs. Latinoamérica).
Biomarcadores (ej. niveles de NT-proBNP, HbA1c, LDL).

Justificación

Puede ayudar a personalizar tratamientos (“medicina de precisión”).
Explora si los beneficios se mantienen en poblaciones diversas.
Identifica posibles riesgos en grupos vulnerables.

Limitaciones y riesgos

Multiplicidad estadística: cada subanálisis aumenta el riesgo de error tipo I (falso positivo).
- Ejemplo: con 20 subgrupos, hay 64% de probabilidad de que al menos uno sea significativo por azar.
Poder estadístico insuficiente: los subgrupos reducen tamaño muestral → intervalos de confianza amplios.
Post hoc vs. preespecificado:
- Preespecificado → más confiable.
- Post hoc → exploratorio, genera hipótesis, no cambia práctica.
Subgrupos absurdos: ISIS-2 (aspirina en IAM) mostró beneficio en todos los subgrupos, incluso “según signo zodiacal” → ejemplo clásico de lo engañoso que puede ser.

Herramienta crítica

Los forest plots suelen resumir análisis de subgrupos.
Pistas de confiabilidad:
- ¿Se reportó valor de interacción (p for interaction)?
- ¿Las diferencias son consistentes en dirección y magnitud?
- ¿Fueron preespecificados en el protocolo?

👉 Regla práctica: solo confiar en subgrupos que fueron preespecificados, clínicamente plausibles y apoyados por evidencia adicional.

2. Análisis por intención de tratar (ITT)

Definición

En ITT, los pacientes se analizan en el grupo al que fueron aleatoriamente asignados, sin importar si:

Recibieron o no el tratamiento.
Abandonaron antes de tiempo.
Cruzaron al grupo contrario.

Fortalezas

Mantiene la aleatorización y evita sesgos de selección.
Refleja la efectividad en condiciones reales (lo que ocurre en la práctica clínica, donde los pacientes no siempre cumplen).
Reduce el optimismo excesivo sobre el fármaco.
Es el estándar en ensayos de superioridad (CONSORT lo recomienda como análisis principal).

Limitaciones

Si hay alto nivel de incumplimiento, puede diluir el efecto verdadero.
Puede subestimar eficacia en pacientes adherentes.

Ejemplo clínico

DAPA-HF (dapagliflozina en IC): análisis ITT demostró beneficio robusto en todos los pacientes asignados, independientemente de adherencia. Esto permitió extrapolar resultados al mundo real.

3. Análisis por protocolo (PP)

Definición

Incluye solo a los pacientes que cumplieron el protocolo tal como fue diseñado, sin desviaciones significativas.

Fortalezas

Estima la eficacia biológica máxima del tratamiento en condiciones ideales.
Útil en ensayos de no inferioridad o equivalencia, donde demostrar un efecto nulo en ITT puede deberse a baja adherencia.

Limitaciones

Rompe el principio de aleatorización → riesgo de sesgo.
Excluye a pacientes con mala adherencia o eventos tempranos, creando una población “seleccionada” poco realista.
Puede sobreestimar eficacia y subestimar efectos adversos.

Ejemplo clínico

Ensayos de anticoagulantes orales directos (NOACs): reportaron tanto ITT como PP. La consistencia entre ambos análisis reforzó la validez de la conclusión de no inferioridad frente a warfarina.

4. Comparación ITT vs. PP

Característica	ITT	PP
Inclusión	Todos los pacientes según asignación original	Solo quienes siguieron el protocolo
Ventaja	Preserva aleatorización, refleja práctica real	Muestra eficacia ideal
Limitación	Dilución del efecto si hay incumplimiento	Sesgo de selección
Uso típico	Ensayos de superioridad	Ensayos de no inferioridad/equivalencia
Recomendación	Siempre análisis principal	Análisis complementario

5. Enfoques modernos

Análisis modificados de ITT (mITT): excluyen ciertos pacientes, ej. los que nunca recibieron ninguna dosis.
Per protocol estricto vs. flexible: algunos protocolos aceptan desviaciones menores.
As-treated analysis: pacientes analizados según lo que realmente recibieron (poco confiable, riesgo alto de sesgo).
Métodos de imputación (ej. Last Observation Carried Forward, MICE): usados para manejar pérdidas de datos en ITT.

6. Ejemplos emblemáticos

HOPE (2000): ITT confirmó beneficio de ramipril en prevención CV, consistente en subgrupos.
ISIS-2 (1988): demostró beneficio de aspirina universal; subgrupos absurdos (signos zodiacales) mostraron los peligros de sobreinterpretación.
CAST (1989): subgrupo de pacientes con supresión de arritmias mostró daño → ejemplo de cómo el desenlace sustituto puede engañar.
RE-LY y ARISTOTLE (ensayos de NOACs): coincidencia entre ITT y PP reforzó no inferioridad frente a warfarina.

7. Lectura crítica práctica

Preguntas que un clínico debe hacerse:

¿El ensayo reportó análisis ITT como principal?
¿Hubo gran número de pérdidas o cruces de grupos?
¿El PP se usó como confirmación o como reemplazo del ITT?
¿Los subgrupos fueron preespecificados en el protocolo?
¿El efecto es consistente en la mayoría de subgrupos clínicamente relevantes?
¿Se reportó “p for interaction” para los subgrupos?

3.5. GRÁFICOS DE SUPERVIVENCIA Y CURVAS DE KAPLAN–MEIER

Introducción

En los ensayos clínicos donde el interés principal es el tiempo hasta un evento clínico (muerte, hospitalización, recaída, progresión de enfermedad), no basta con reportar la proporción de pacientes con evento al final del seguimiento.

Se necesita una técnica que:

Tenga en cuenta el momento exacto en que ocurren los eventos.
Permita manejar datos de pacientes que no completaron el seguimiento (censura).
Compare de manera justa las probabilidades de supervivencia entre grupos.

Para ello se utilizan los gráficos de Kaplan–Meier (K–M), una de las representaciones más influyentes en medicina moderna.

👉 Estas curvas muestran la dinámica del riesgo a lo largo del tiempo, revelando si el beneficio de una intervención es inmediato, sostenido o variable.

Breve historia

Edward Kaplan y Paul Meier (1958): introdujeron la técnica estadística que revolucionó la forma de presentar datos de supervivencia.
Antes, solo se reportaba la mortalidad final, ignorando el tiempo hasta el evento y las pérdidas de seguimiento.
Hoy, las curvas K–M son estándar en prácticamente todos los ensayos clínicos de supervivencia, oncología, cardiología e infectología.

Fundamentos estadísticos

La función de supervivencia se define como:

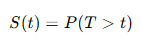
Es decir, la probabilidad de que un paciente permanezca libre de evento más allá del tiempo ttt.

Características técnicas:

Método no paramétrico: no requiere suponer una distribución específica de los tiempos.
Escalones descendentes: cada evento (ej. muerte) hace que la curva baje en un “escalón”.
Censura: pacientes que salen del estudio sin evento (pérdida, retiro, fin del seguimiento) → representados con una marca (+).
Tabla de “número en riesgo”: se coloca bajo la gráfica para mostrar cuántos pacientes seguían en observación en cada punto de tiempo.

Interpretación de una curva Kaplan–Meier

Separación de curvas
- Si ocurre pronto → beneficio temprano (ej. antiagregantes en IAM).
- Si ocurre tardíamente → beneficio acumulativo (ej. estatinas en prevención secundaria).
- Si se cruzan → puede indicar efectos opuestos en diferentes periodos (ej. toxicidad inicial vs. beneficio a largo plazo).
Magnitud del efecto
- La distancia vertical entre curvas refleja el tamaño de la diferencia en supervivencia.
Pruebas estadísticas asociadas
- Log-rank test: compara si existe diferencia global entre las curvas.
- Hazard Ratio (HR): cuantifica el riesgo relativo a lo largo del tiempo, con IC95%.
Precisión y confiabilidad
- Si al final del seguimiento quedan pocos pacientes, la curva pierde estabilidad.
- Por eso es fundamental mirar la tabla de pacientes en riesgo.

Ejemplos clínicos

Cardiología

DAPA-HF (2019): las curvas de supervivencia se separaron precozmente mostrando reducción en muerte CV y hospitalización por IC con dapagliflozina.
SOLVD (1991): demostró que enalapril prolongaba la supervivencia en IC crónica, con separación clara y sostenida de curvas.

Oncología

KEYNOTE-189: en cáncer de pulmón, pembrolizumab mostró separación progresiva de curvas, con beneficio de largo plazo en supervivencia global.

Infectología

RECOVERY (2020, dexametasona en COVID-19): curvas de K–M demostraron reducción clara de mortalidad en pacientes ventilados, cambiando guías globales.

Fortalezas y limitaciones

Fortalezas

Representan todo el seguimiento, no solo un “punto final”.
Manejan la censura de forma adecuada.
Permiten identificar patrones temporales del efecto (temprano, tardío, sostenido).

Limitaciones

Su interpretación asume proporcionalidad de riesgos (fundamento del HR).
Si las curvas se cruzan, el HR global puede ser engañoso.
Requieren gran número de pacientes en riesgo al final para evitar inestabilidad.
No traducen directamente a métricas aplicables como el NNT.

Errores comunes en la interpretación

Concluir que existe beneficio porque las curvas “parecen separarse” sin respaldo del log-rank o HR.
Ignorar los cruces de curvas, que pueden señalar toxicidad o subgrupos diferentes.
No revisar cuántos pacientes siguen en riesgo al final → curvas finales pueden ser ilusorias.
Interpretar el HR como constante en todo el seguimiento, cuando en la práctica el efecto puede variar.

Herramienta práctica de lectura crítica

Cuando analices una curva K–M, pregúntate:

¿Las curvas se separan claramente y en qué momento ocurre?
¿El HR y su IC95% apoyan la diferencia visualizada?
¿Hay cruces que compliquen la interpretación?
¿El beneficio mostrado es clínicamente relevante o solo estadísticamente significativo?
¿Cuántos pacientes seguían en riesgo en los puntos finales del gráfico?

Descubre más desde Medicina Cardiometabólica

Suscríbete y recibe las últimas entradas en tu correo electrónico.