Análisis Exploratorio y Correlación

📊 1. Tablas de Contingencia en STATA

Las tablas de contingencia permiten resumir datos de forma comparativa entre grupos. En esta práctica, vamos a utilizar dos comandos fundamentales:

🔸 A. `tabstat`: Estadísticas por grupo

📌 Objetivo: Obtener estadísticas resumidas (media, desviación estándar, mínimo y máximo) de variables continuas según un grupo categórico.

* Estadísticas de glucosa, edad y peso por sexo
tabstat glucosa edad peso, by(sexo) statistics(mean sd min max)

✅ Interpretación didáctica:
Compara el promedio y la variabilidad entre hombres y mujeres. Por ejemplo:

¿Tienen los hombres mayor glucosa promedio que las mujeres?
¿Qué grupo tiene mayor variabilidad en el peso?

🔸 B. `table`: Cruce de variables categóricas

📌 Objetivo: Ver la frecuencia absoluta y/o porcentajes entre dos variables categóricas (por ejemplo, sexo e hipertensión).

* Tabla simple: número de personas por sexo e hipertensión
table sexo hipertenso

* Agregar porcentajes por fila
table sexo hipertenso, statistic(freq row)

✅ Interpretación didáctica:
Observamos cómo se distribuyen los hipertensos entre hombres y mujeres.
¿Hay más mujeres con hipertensión en proporción? ¿O más hombres?

🧪 2. Pruebas de Normalidad en STATA

📌 ¿Cuándo se usan?

Antes de hacer comparaciones de medias o correlaciones paramétricas, debemos saber si nuestras variables tienen distribución normal. Para ello usamos:

Comando	Prueba	Usar cuando…
`swilk`	Shapiro-Wilk	Muestras pequeñas (< 2000)
`sktest`	Asimetría y curtosis combinadas	Muestras medianas y grandes (> 20)

🔸 A. Shapiro-Wilk (`swilk`)

* Prueba de normalidad para la variable glucosa
swilk glucosa

✅ Interpretación:

p > 0.05 → Distribución normal (no se rechaza H₀)
p < 0.05 → No normal (se rechaza H₀)

🔸 B. Skewness/Kurtosis Test (`sktest`)

* Prueba alternativa de normalidad
sktest glucosa

✅ Interpretación:

También ofrece p-valor global para normalidad.
Si alguna de las subpruebas (asimetría o curtosis) sale significativa, puede indicar no normalidad.

🎯 Reglas prácticas para revisión rápida:

Asimetría entre -0.5 y +0.5 → simetría aceptable
Curtosis entre 2.5 y 3.5 → distribución no excesivamente picuda ni plana
p > 0.05 (en Pr(Skewness), Pr(Kurtosis) y chi²) → normalidad aceptada

📊 Extra: Histograma para visualización

* Histograma con curva normal
histogram glucosa, normal

👀 Interpretación visual: Compara la forma de los datos reales con la curva normal.

📝 Actividad para estudiantes

Aplicar swilk y sktest a las variables: glucosa, colesterol, presión sistólica.
Determinar si pueden aplicar t-test o deben usar pruebas no paramétricas.
Interpretar y comentar:
- ¿Cuál variable se aleja más de la normalidad?
- ¿Qué análisis paramétricos podrían no ser válidos?

📌 Interpretación general del p-valor:

p > 0.05 → No hay evidencia contra la normalidad → ✅ Datos normales
p ≤ 0.05 → Se rechaza la normalidad → ⚠️ Datos no normales

✅ Si los datos son normales (p > 0.05 en pruebas de normalidad)

🔹 Puedes usar pruebas paramétricas
Estas pruebas asumen normalidad y tienen mayor poder estadístico si se cumplen sus supuestos.

Objetivo del análisis	Prueba paramétrica
Comparar 2 grupos	t de Student (t-test)
Comparar > 2 grupos	ANOVA
Correlación	Pearson
Asociación entre variables	Regresión lineal

⚠️ Si los datos NO son normales (p ≤ 0.05)

🔹 Usa pruebas no paramétricas
Estas no requieren normalidad y son más robustas ante datos con asimetría o valores extremos.

Objetivo del análisis	Prueba no paramétrica
Comparar 2 grupos	Mann-Whitney U / Wilcoxon
Comparar > 2 grupos	Kruskal-Wallis
Correlación	Spearman
Asociación entre variables	Regresión no paramétrica / modelos robustos

🧠 Tips prácticos:

Si tienes n > 30–40, muchas veces las pruebas paramétricas se pueden usar igual (por el teorema central del límite), pero debes justificarlo.
Si tienes valores atípicos, conviene usar no paramétricas o transformar los datos.
Siempre acompaña con gráficos (boxplot, histogramas, Q-Q plot) para reforzar tu decisión.

🔗 3. Correlación en STATA

La correlación evalúa la fuerza y dirección de la relación entre dos variables numéricas. Existen dos tipos principales:

Tipo	Comando	Uso recomendado
Pearson	`pwcorr`	Variables con distribución normal
Spearman	`spearman`	Variables no normales o con outliers

🔸 A. Correlación de Pearson – `pwcorr`

* Correlación entre edad, presión sistólica y colesterol
pwcorr edad presion_sys colesterol, sig star(0.05)

✅ Interpretación:

Los valores van de -1 a +1
Positivo: a mayor edad, mayor presión.
Negativo: a mayor edad, menor colesterol.
sig muestra los p-valores.
star(0.05) pone * donde la correlación es significativa.

✅ Interpretación general:

Todas las correlaciones son positivas, fuertes (cercanas a 1) y estadísticamente significativas (p < 0.05).
El asterisco * indica que estas asociaciones tienen evidencia estadística para ser consideradas reales y no producto del azar.

✅ ¿Qué hace cada parte?

Parte del comando	Función
`pwcorr`	Calcula correlaciones de Pearson entre pares de variables
`sig`	Muestra el p-valor asociado a cada correlación
`star(0.05)`	Agrega un *asterisco `` si el p-valor es menor a 0.05** (significativo)

🔸 B. Correlación de Spearman – `spearman`

stataCopiar código* Correlación no paramétrica entre glucosa y edad
spearman glucosa edad

✅ Interpretación:

Similar a Pearson, pero basada en rangos.
Útil cuando las variables no son normales o tienen outliers.

🧪 Recomendación antes de correlacionar:

👉 Verifica la normalidad de ambas variables
👉 Considera gráficos de dispersión:

* Diagrama de dispersión
scatter glucosa edad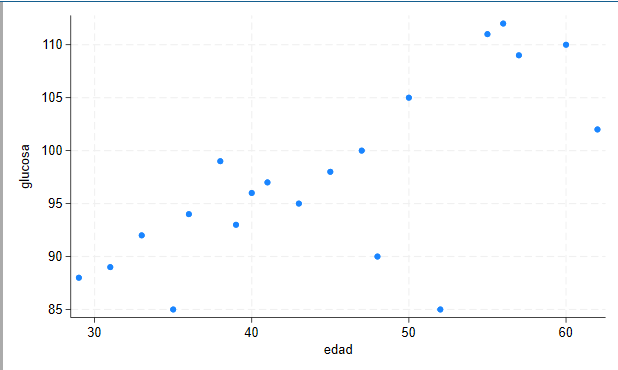

Es probable que exista una correlación positiva significativa entre edad y glucosa.

📝 Actividad para estudiantes

Usar pwcorr para evaluar:
- edad y presión sistólica
- edad y colesterol
Usar spearman si alguna de las variables no es normal.
Responder:
- ¿Qué par de variables muestra la mayor correlación?
- ¿La correlación es positiva o negativa?
- ¿Es estadísticamente significativa?

⚖️ 4. Comparación de Medias en STATA

La prueba t de Student compara si dos grupos (definidos por una variable categórica binaria) tienen promedios diferentes en una variable numérica.

📌 Sintaxis general:

ttest <variable_continua>, by(<grupo_binario>)

🔸 A. Comparar glucosa entre hipertensos y no hipertensos

ttest glucosa, by(hipertenso)

✅ Interpretación:

Compara las medias de glucosa entre personas con y sin hipertensión.
Si p < 0.05, hay diferencia estadísticamente significativa entre grupos.

✅ Resultados de la prueba:

Hipótesis nula (H₀): No hay diferencia en los niveles de glucosa entre grupos.
t = -3.4023
p-valor (Pr(|T| > |t|)) = 0.0032 → Significativo
Intervalo de confianza del 95% para la diferencia: [-16.8286, -3.9795] → no incluye 0

🧠 Conclusión:

✔️ Diferencia significativa en los niveles de glucosa entre personas hipertensas y no hipertensas.
❗Las personas hipertensas tienen niveles más altos de glucosa en promedio.
Como p < 0.05, se rechaza la hipótesis nula.

🔸 B. Comparar colesterol por sexo

ttest colesterol, by(sexo)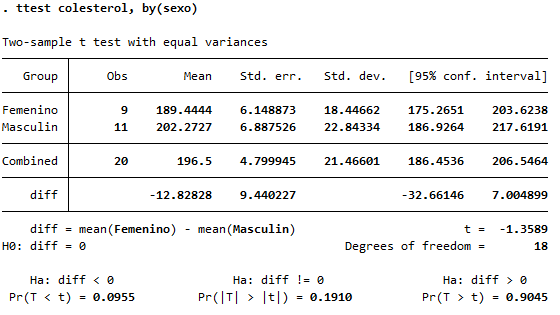

✅ ¿Cuándo es válido usar t-test?

Cuando la variable continua tiene distribución normal en ambos grupos.
Si no hay normalidad, usar test no paramétrico como ranksum.

✅ Resultados del test:

t = -1.3589
p-valor (Pr(|T| > |t|)) = 0.1910 → ❌ No significativo
Intervalo de confianza del 95% para la diferencia: [-32.66, 7.00] (incluye el 0)

🧠 Conclusión:

❌ No hay diferencia estadísticamente significativa en los niveles de colesterol entre hombres y mujeres en esta muestra.
Aunque los varones tienen un promedio mayor, el p-valor > 0.05 y el intervalo de confianza incluye el 0, por lo tanto, no se rechaza la hipótesis nula.
Puede haber diferencia real, pero no es estadísticamente detectable con esta muestra (posible tamaño pequeño).

🔧 Si no cumple normalidad:

ranksum glucosa, by(hipertenso)

z = -2.812
p-valor aproximado = 0.0049
p exacto = 0.0032 → ✅ significativo

✅ Conclusión:

p < 0.05 → se rechaza la hipótesis nula.
Existe una diferencia estadísticamente significativa en los niveles de glucosa entre hipertensos y no hipertensos.
Los hipertensos tienden a tener mayor glucosa (porque sus rangos son más altos).

🧠 ¿Cuándo usar esta prueba?

Se usa cuando:

❌ Los datos no cumplen normalidad o hay valores atípicos.
✅ Quieres una prueba robusta que no dependa de la distribución.

📈 Visualización adicional (opcional)

graph box glucosa, over(hipertenso)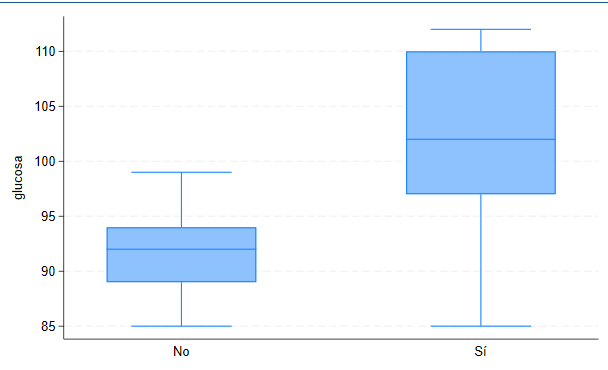

👀 Esto te muestra gráficamente las diferencias de medias y rangos.

📝 Actividad para estudiantes

Comparar la media de:
- glucosa por hipertensión
- colesterol por sexo
Evaluar si las diferencias son significativas (p < 0.05).
Responder:
- ¿Qué grupo tiene mayor media?
- ¿La diferencia es clínicamente relevante?
- ¿Se cumplió la normalidad antes de usar ttest?