Cómo interpretar un forest plot?

A medida que nos acercamos a la cima de la pirámide de la medicina basada en la evidencia, a veces surgen gráficos de aspecto extraño. El diagrama de bosque es una forma clave en que los investigadores pueden resumir datos de varios artículos en una sola imagen. 

Figura 1. Un ejemplo de parcela forestal. Imagen adaptada de la Tabla 4 Roberts et al. (2006). [1]Como estudiantes, a veces pensamos que gráficos como el de la figura 1 son un poco difíciles de interpretar. No temas: ¡el siguiente tutorial te mostrará paso a paso cómo interpretar cualquier diagrama de bosque!

Información tutorial

Objetivos de aprendizaje.
Al final de este tutorial deberías poder:

1. Comprender para qué se utilizan los forest plot
2. Comprender cómo leer un diagrama de bosque y qué significan los resultados mostrados tanto a nivel de estudios individuales como del resultado promedio.
3. Comprender por qué los diagramas forestales se ven diferentes según las estadísticas que se analizan
4. Comprender la importancia de la heterogeneidad dentro de las parcelas forestales y cómo afecta la interpretación.

Tiempo para completar el tutorial: 20-30 minutos
Preguntas de ejemplo: Sí
Referencias todas de acceso abierto: Sí

Entonces, ¿por qué hacer un forest plot en primer lugar?

Tratar de mirar muchísimos artículos diferentes que plantean la misma pregunta puede resultar difícil. Esto es especialmente cierto si los artículos analizados llegan a conclusiones diferentes y tienen estadísticas diferentes a favor o en contra de una asociación.

Lo que hace un diagrama de bosque es tomar todos los estudios relevantes que hacen la misma pregunta, identifica una estadística común en dichos artículos y los muestra en un único conjunto de ejes. Hacer esto le permite comparar directamente lo que muestran los estudios y la calidad de ese resultado, todo en un solo lugar. 

Análisis de la parcela forestal: conceptos básicos

Parte 1: El eje.

A lo largo de este tutorial tomaremos como ejemplo la Figura 1 (que se muestra arriba), un diagrama de bosque de una revisión sistemática Cochrane. A medida que avancemos en el tutorial, construiremos la Figura 1 a partir de los primeros principios. ¡Revelaré el significado de este bosque en particular al final del blog!

Figura 2. Tomemos esto desde el principio.

Lo que ves a la izquierda es el conjunto básico de ejes que emplean los diagramas forestales. El eje horizontal suele representar la estadística que muestran los estudios que se perfilan. Esto podría ser una estadística «relativa» como un odds ratio (OR) o un riesgo relativo (RR). O las estadísticas utilizadas podrían ser «absolutas», como la Reducción Absoluta del Riesgo (ARR) o la Diferencia de Medias Estandarizada (SMD). Conocer la diferencia entre estadísticas relativas y absolutas es importante porque afecta qué número se encuentra en la línea vertical.

La línea vertical se conoce como “línea de efecto nulo”. Esta línea se coloca en el valor donde (como sugiere el título) no hay asociación entre una exposición y un resultado o no hay diferencia entre dos intervenciones. Si recuerda de sus clases de estadística, las estadísticas relativas como OR o RR tienen un valor de efecto nulo de 1. Para estadísticas absolutas como Riesgo absoluto o ARR o SMD, el valor de diferencia nula es 0. De ahí el valor en la línea sin efecto. es relevante para la estadística que se utiliza. Si desea un repaso sobre las estadísticas relativas y absolutas , ¿por qué no consulta este blog de S4BE ?

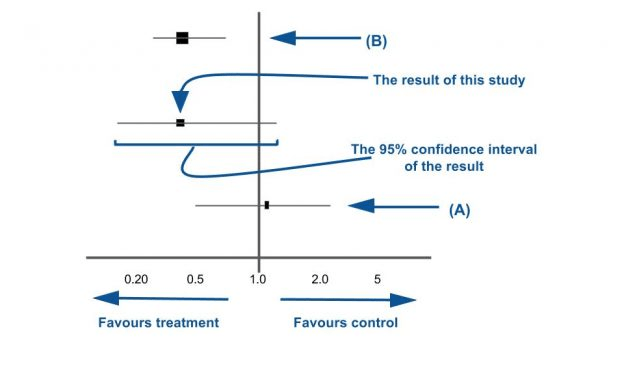
Figura 3. Pongamos unas líneas sobre estos ejes.

Parte 2: Las líneas de estudio. 

Bien, ahora que entendemos los ejes del diagrama de bosque, pongamos algunos valores. Cada línea horizontal colocada en una parcela forestal representa un estudio separado que se está analizando. En la Figura 3 se representan tres estudios. Cada «resultado» de un estudio tiene dos componentes:

1. Una estimación puntual del resultado del estudio representada por un cuadro negro. Este cuadro negro también ofrece una representación del tamaño del estudio. Cuanto más grande sea la caja, más participantes habrá en el estudio.
2. Una línea horizontal que representa los intervalos de confianza del 95 % del resultado del estudio, y cada extremo de la línea representa los límites del intervalo de confianza.

Lo que representa cada lado de la línea del efecto nulo (es decir, si favorece el control o la intervención) también es importante cuando se analizan los estudios individuales. Esto será diferente dependiendo de la pregunta que hagas en tus estudios. Por ejemplo, si observa el riesgo entre una exposición y un resultado, lo que representa cada lado de la línea vertical será diferente a un caso en el que compara una intervención con un control. Es útil que en la mayoría de los diagramas forestales publicados hoy los autores marquen lo que representa cada lado de la línea. Si no está marcado, recuerde volver siempre a los principios básicos de la estadística que está utilizando.

Es particularmente importante tomar nota de la línea horizontal y si cruza la “línea de efecto nulo” para cada estudio. Si recuerda, la definición increíblemente básica del intervalo de confianza del 95% es: » El rango de valores dentro del cual puede tener un 95% de certeza sobre el valor verdadero «. Si la línea horizontal cruza la línea de efecto nulo, lo que eso significa efectivamente es que el valor nulo se encuentra dentro de su intervalo de confianza y, por lo tanto, podría ser el valor verdadero. Si estuviera descomponiendo esto en su explicación más simple: » cualquier línea de estudio que cruce la línea del efecto nulo no ilustra un resultado estadísticamente significativo «.

Hay un componente más en la línea del que es útil tomar nota. Aunque no está garantizado, como regla general los estudios con un  mayor número de participantes o pacientes suelen tener un  intervalo de confianza más estrecho y, por tanto, una línea horizontal más pequeña. Entonces en términos básicos:

1. Cuanto más grande es el estudio, más pequeña es la línea horizontal y más grande es el cuadro negro que representa la estimación puntual. Esto puede significar que es menos probable que esos estudios crucen la línea del efecto nulo. ¿Por qué? Porque sus intervalos de confianza del 95% deberían tener un rango mucho más pequeño.
2. Cuanto más pequeño sea el estudio, más ancha será la línea horizontal y más pequeño será  el cuadro negro que representa la estimación puntual. Esto significa que es más probable que esos estudios crucen la línea del efecto nulo (porque sus intervalos de confianza del 95% serán mucho mayores).

Ahora que ha leído la descripción anterior, eche un vistazo al Estudio (A) y al Estudio (B) en la Figura 3. Intente interpretar lo que cada estudio le dice antes de buscar la respuesta en la parte inferior de la página web.

Parte 3: Combinando todos los estudios de la parcela forestal.

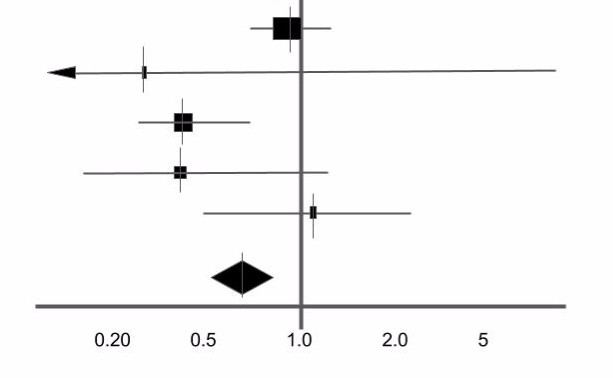
Figura 4. El Diamante del grupo.

La Figura 4 agrega dos estudios más en la parte superior (intenta interpretarlos), así como un diamante. Ahora bien, el diamante es probablemente lo más importante que verá en un terreno forestal.

El diamante representa la estimación puntual y los intervalos de confianza cuando se combinan y promedian todos los estudios individuales. Si dibujó una línea vertical a través de los puntos verticales del diamante, eso representa la estimación puntual de los estudios promediados. Los puntos horizontales del diamante representan el intervalo de confianza del 95% de esta estimación puntual combinada. Si recuerda lo que dije en la parte 2 sobre el tamaño de los intervalos de confianza, debido a que este valor combinado agrupa efectivamente  a todos los participantes de todos  los estudios individuales, el rango de IC para este resultado debe ser el más pequeño en el diagrama de bosque (y en 99 % de casos normalmente lo es).

Las reglas sobre cruzar la línea de efecto nulo siguen siendo válidas aquí: si las puntas horizontales del diamante cruzan la línea vertical, el resultado combinado potencialmente no es estadísticamente significativo. ¿Por qué? Si recuerda, si el intervalo de confianza del 95% contiene el valor nulo, no puede estar seguro de que el valor nulo no sea el valor verdadero.

Parte 4: Reuniéndolo todo.

Por eso hemos hablado de varios elementos de la propia parcela forestal. Echemos un vistazo a todos los «bumf», por así decirlo, que se encuentran alrededor del diagrama de bosque en el gráfico. Volvamos a nuestra imagen original. Las Figuras 5 a 8 resaltan diferentes elementos del diagrama de bosque que vale la pena señalar.

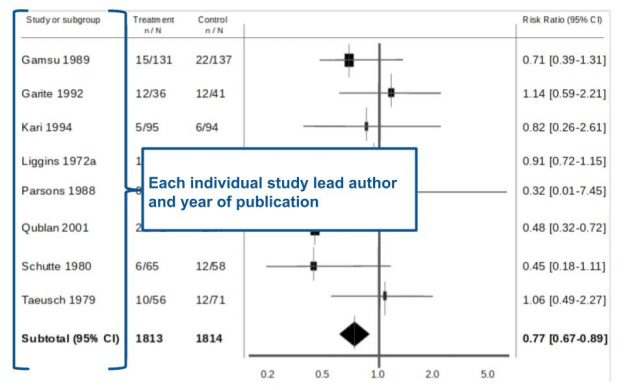
Figura 5. Hay mucha información además de la trama misma.

En la Figura 5, en el extremo izquierdo del diagrama de bosque, se encuentra el nombre del autor principal de cada estudio individual, así como el año de publicación.

Inmediatamente a la izquierda del diagrama de bosque, hay dos columnas de números, resaltadas en la Figura 6. Cada columna de números tiene dos números separados por una ‘/’. Si observa el encabezado de cada columna, verá que los números están organizados como «n/N». ¿Qué quiere decir esto? En pocas palabras, ‘n’ denota el número de pacientes o individuos que tuvieron el evento/resultado en ese grupo en particular, mientras que ‘N’ denota el número total de personas en ese grupo.

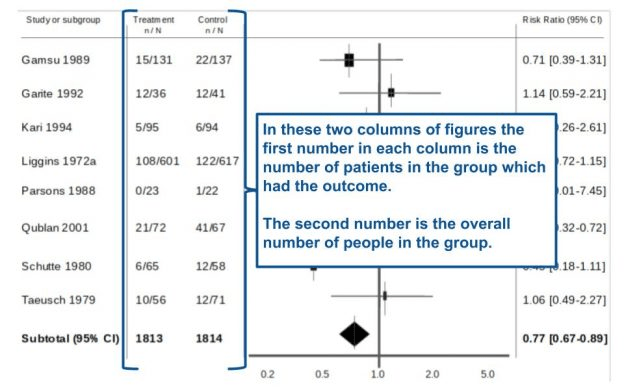
Figura 6. Tiene sentido cuando comparas los números con el gráfico.

Entonces, en nuestro artículo de ejemplo tenemos dos columnas de números. La primera columna es para el grupo que recibió el tratamiento (n= número de personas tratadas que obtuvieron resultados, N= número total de personas en el estudio que recibieron tratamiento). Mientras que la segunda columna es para el grupo que obtuvo el control (n= número de personas en el grupo de control que tuvieron resultados, N= número total de personas que estaban en el grupo de control).

Figura 7. A veces es más sencillo comparar los números…

La Figura 7 está al otro lado de la parcela forestal. La columna del extremo derecho básicamente le brinda el diagrama de bosque como números (tanto la estimación puntual como el intervalo de confianza del 95% entre paréntesis). A algunas personas les puede resultar más fácil mirar directamente estos números en lugar de mirar la trama e intentar interpretarla.

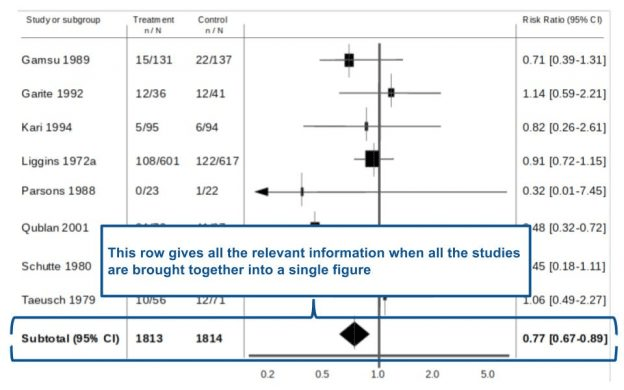
Figura 8. Si está en negrita, ¡probablemente haya una razón para ello!

Figura 8: Esto simplemente resalta las estadísticas asociadas con el diamante en la parcela forestal. El ‘subtotal’ es lo que dice en la lata. Le indica el número total de participantes en los grupos de tratamiento y control en todos los estudios individuales, así como la estadística promedio y el intervalo de confianza del 95%. Es útil observar esta línea de números y el diamante al sacar conclusiones para su metanálisis/revisión sistemática.

Parte 5: Heterogeneidad de los artículos.

La parte final del análisis de una parcela forestal consiste en observar algo llamado «heterogeneidad». Idealmente, si diferentes ensayos prueban lo mismo, los efectos de la intervención/exposición deberían ser consistentes en todos los estudios. Por desgracia, esto no suele ser el caso. Muchas cosas pueden afectar los resultados de un ensayo, como el sesgo del investigador o problemas con la recopilación de datos [2].

Entonces, además de analizar los resultados del estudio, las revisiones sistemáticas o metanálisis están diseñados para formular una pregunta. Si todos estos estudios prueban la misma intervención, ¿por qué no obtienen los mismos resultados? ¿Las diferencias son causadas por el azar o hay algo más involucrado? Si es casualidad, entonces no tenemos nada de qué preocuparnos. Si las diferencias no son resultado del azar, entonces debemos ser cautelosos al interpretar los resultados. Para facilitar la evaluación de la coherencia de los artículos analizados, se utiliza una estadística denominada I ²  (‘i-cuadrado’).

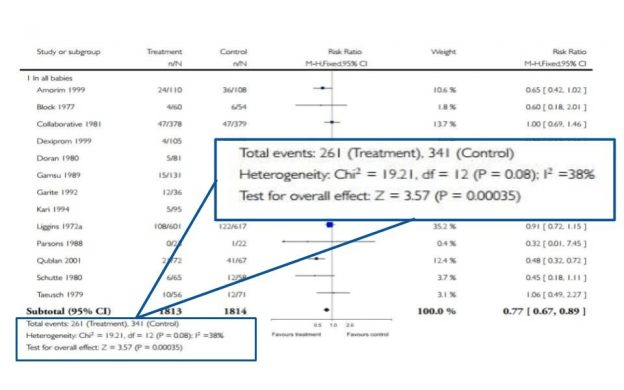
Figura 9. Veo, veo con mi ojito… algo que comienza con h…

Como muestra la Figura 9, las estadísticas relacionadas con la heterogeneidad suelen estar en la parte inferior del gráfico. La regla general es que desea que I ² sea inferior al 50%. Cualquier valor superior a eso y los documentos podrían ser inconsistentes debido a alguna razón distinta al azar (¡lo cual es malo!). Para nuestro ejemplo, afortunadamente, el I ² es del 38%; no es perfecto, pero aún está dentro de nuestro rango objetivo. Notarás que hay otras estadísticas como Chi ² y z. Para los propósitos de este tutorial, I ² es el más útil para interpretar un diagrama de bosque.

Resumen

Con suerte, revisar una parcela forestal de principio a fin le ha ayudado a comprender qué es lo que hace que las parcelas forestales funcionen. Realmente lo animo a que se desplace hasta la parte superior y mire la Figura 1, que no tiene ninguna anotación, y siga los 5 pasos que hemos seguido.

Para resumir lo que hemos cubierto:

1. Cada línea horizontal en un diagrama de bosque representa un estudio individual con el resultado representado como un cuadro y el intervalo de confianza del 95% del resultado mostrado como la línea.
2. La implicación de que cada estudio caiga de un lado u otro de la línea vertical depende de la estadística que se utilice.
3. Si el estudio individual cruza la línea vertical, significa que el valor nulo se encuentra dentro del intervalo de confianza del 95%. Esto implica que el resultado del estudio es, de hecho, el valor nulo y, por lo tanto, el estudio no observó una diferencia estadísticamente significativa entre los grupos de tratamiento y control.
4. El diamante en la parte inferior del diagrama de bosque muestra el resultado cuando todos los estudios individuales se combinan y se promedian. Los puntos horizontales del diamante son los límites de los intervalos de confianza del 95% y están sujetos a la misma interpretación que cualquiera de los otros estudios individuales en el gráfico.
5. La estadística I ² da una idea de la heterogeneidad de los estudios, es decir, de su coherencia. Si el valor de I ² es >50%, podría significar que los estudios son inconsistentes debido a una razón distinta al azar. Esto podría hacer que las conclusiones que saque del diagrama del bosque sean cuestionables.

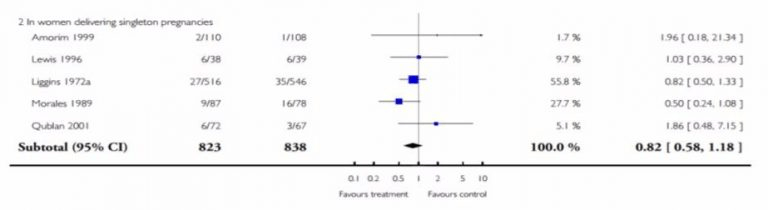
Figura 10. Otro diagrama de bosque del mismo artículo para trabajar. Imagen de Roberts et al. (2006) [1]

¿Tener sentido? ¡Eso espero! Si desea trabajar con otro ejemplo, eche un vistazo a la Figura 10: un diagrama de bosque del artículo del que proviene la Figura 1. ¿Cuál es el significado de la Revisión Cochrane que insinué al principio? Quizás se pregunten.

Y finalmente…

Bueno, si alguna vez ha visto el logotipo de la Colaboración Cochrane, es posible que reconozca las líneas horizontales y el diamante.

Esto se debe a que el logotipo de la Colaboración Cochrane es en realidad la representación de una parcela forestal. El diagrama de bosque en el logotipo de la Colaboración Cochrane proviene de una de las primeras revisiones sistemáticas jamás publicadas [3]. El artículo, publicado en 1991, demostró que administrar esteroides a las madres cuyos bebés iban a nacer prematuramente reducía las complicaciones de la prematuridad. La revisión Cochrane de la que provienen las Figuras 1 y 10 es en realidad una actualización de esa revisión original que formó el logotipo de la Colaboración Cochrane.

Referencias:

[1]  Roberts D , Dalziel SR . Corticosteroides prenatales para acelerar la maduración pulmonar fetal en mujeres con riesgo de parto prematuro . Base de datos Cochrane de revisiones sistemáticas 2006 , número 3 . Arte. No.: CD004454.
[2] “Cómo analizar el diagrama de bosque: evaluar la heterogeneidad entre los estudios”. Centro de Intervención Basada en Evidencia, Universidad de Oxford. URL:  http://www.cebi.ox.ac.uk/for-practitioners/what-is-good-evidence/how-to-interpret-the-sample-forest-plot.html#c56 Consultado: junio de 2016
[ 3] “Nuestro logotipo: Colaboración Cochrane”. La Colaboración Cochrane, 2016. URL:  http://www.cochrane.org/about-us/our-logo . Consultado: junio de 2016.

Parte 2 RESPUESTAS: ¡NO MIRES HASTA HABER PROBADO!

Entonces, ¿cómo te fue? Lo que con suerte deberías haber encontrado es:

• Para el estudio A, tiene una línea horizontal bastante ancha que cruza la línea de efecto nulo con un cuadro negro que está a la derecha de la línea vertical. Lo más probable es que esto demuestre un estudio a pequeña escala con pocos participantes donde el resultado de la estimación puntual favorece el control utilizado en el estudio. Pero debido a que el estudio contiene el valor nulo en su intervalo de confianza del 95%, es probable que tenga un valor de p >0,05 y no sea estadísticamente significativo.
• Para el estudio B, tiene una línea bastante estrecha que no cruza la línea de efecto nulo con un cuadro negro que está a la izquierda de la línea vertical y es más grande que el estudio A. Lo más probable es que esto demuestre un estudio más grande con más participantes en comparación. al estudio A, donde el resultado favorece la intervención utilizada. Debido a que el intervalo de confianza del 95% no contiene el valor nulo, es probable que este estudio tenga un valor de p <0,05 y, por lo tanto, las diferencias observadas en el estudio pueden considerarse estadísticamente significativas.

TRADUCIDO DE: https://s4be.cochrane.org/blog/2016/07/11/tutorial-read-forest-plot/